What is logarithmic

What's logarithmic?

The logarithm is a function that was devised to find complex multiplications and divisions roughly (i.e. not exactly, but reasonably close) by addition and subtraction. Originally there was an attempt to calculate the orbits of the planets in the solar system and to find the laws. This is now known as Kepler's laws. This was a tricky calculation because of the number of digits and the number of times it had to be done. There were no calculators in those days, and multiplication, let alone addition, was a very time-consuming task.
To digress for a moment, why were we trying to calculate the orbits? Because planets, as their name implies, move in a strange way that is different from that of other stars, and if we assume that the earth is the centre of the universe (the theory of celestial motion), we need a complex model to explain their movements. It turns out that if we assume that the Earth, like the planets, orbits the Sun, then the seemingly complex motions can be easily explained. It was this mathematical clarity that saved the Church from a trial.
But back to the story. Nowadays, logarithms are used to show the relationship between some number and a parameter with different digits. For example, in the Tsugu graph, the horizontal axis goes from 10-9m to 10-2m, but if you try to draw it on a graph with a normal scale, you won't be able to do it at all. The various properties of the logarithmic function are also essential for the theoretical analysis of various phenomena.

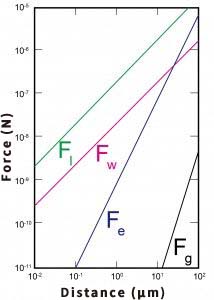
For the sake of logarithms, let's go back to orbital calculations for a moment. In those days, orbital calculations involved a lot of multiplication, so they used the sum-of-products formula for trigonometric functions (which you'll find below) to convert multiplication into addition.

When you see the word trigonometric function, you may say "I don't understand". Trigonometric functions were invented, however, to express the relationship between one of the other two interior angles in a right triangle (the sum of the interior angles is 180°, so one of them is sufficient) and the ratio of the lengths of the two sides. (It is a function of the angle, since the value is determined by the angle as a parameter.)
In this case, there are only three possible combinations of edges: the hypotenuse and the height, the hypotenuse and the base, and the base and the height. This ratio (e.g. the ratio of the lengths of the hypotenuse to the base) is constant with the angle (and does not depend on the size of the triangle). Similarity. ) The value changes slightly as the angle changes. The table of trigonometric functions is a summary of these changes. For your information, the ratio of the slope to the height is called sine, the ratio of the slope to the length of the base is called cosine, and the ratio of the length of the base to the height is called tangent.



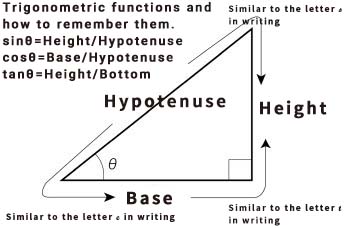
If the length of the diagonal is 1 (or cm, or m, or whatever), then the lengths of the height and base at a certain angle are the respective sin and cos values at that angle. Simple, isn't it? But this simple relationship is one of the foundations of modern science. It is essential for the principles and calculations of rotational motion, electricity, flow, image compression [PC, TV, etc.], etc.

Now, in order to calculate multiplication by addition, they used trigonometric functions to calculate it as follows. The sum-of-products formula that they used to calculate looks like this,

sinA×sinB = -(cos(A+B)-cos(A-B))÷2　　, which A&B means angle, respectivelly

This means that you can calculate the multiplication on the left by adding and subtracting on the right (some division is involved, but it's easy because it's just dividing by two). But how can this be used to calculate normal multiplication? But how can this be used to calculate normal multiplication?

Let's write it down concretely. First, we need to make sure that the number we want to multiply is between 0 and 1, or some number 0. (For example, 6091 x 14527 would be 0.6091 x 10⁴ and 0.1453 x 10⁵. Here we have aligned the significant figures to four digits). Next, from the sin column of the trig table, find the closest one to each decimal point and read the corresponding angle (find A and B). Having read the two angles, we calculate the sum and difference of the two angles and find the value of cos for each angle in the table of trigonometric functions. Subtract each of the cos values and divide by two. Finally, if we add back the digits that we had to divide to get the first digit down (in this case 10⁴ x 10⁵ = x 10⁹ times), we can calculate the multiplication by addition and subtraction.
This method only gives the correct result for the significant figures, but in the old days multiplication was very difficult, so it was a good way of doing it, even with trigonometric tables, just by adding and subtracting (in the sum-of-products formula you divide by two at the end, but this is easy because you only have to halve).

However, it is tedious to use the formula just for the sake of calculation. It is also tedious because you have to find the angle from the value of sin twice, and find the value of cos from the two angles twice, i.e. four times in the table.

This led to the idea of logarithms.
The textbook says,
When y^x = z, then x = log_yz
The function logyz is defined as the logarithm, and is called the normal logarithm, especially when y is 10. And it has various properties, I think. I think this is the correct way to explain mathematics, but I think people often think that they don't know what it's for. (Although some of them emphasise the connection with exponents.)
Using the properties of logarithms, multiplication and division (which can be calculated by subtraction in logarithms) can be carried out by addition and subtraction. To do this, we use the logarithmic formula log xy=log x+log y in a similar way to the sum of products formula for trigonometric functions. First, we read the values of the logarithms of x and y from a logarithm table. Find the value of xy that is equal to or close to the sum of those values (i.e. log x and log y) in the logarithm table, and then subtract back the number that would give that value.
By the way, logarithms were invented (published) at the beginning of the 17th century, in 1614, and the ordinary logarithm table was made three years later (it was easy to use the table, but it took a very long time to make it).
However, it was difficult to carry the tables around with you, and it was also troublesome to find the numbers in the tables and to add them up, so an instrument was invented that looked like a ruler and made it easy to calculate with logarithms. This is called a tape measure.
However, it is difficult to carry a table around with you, and it is cumbersome to find the numbers in the table and to add them up, so an instrument was invented which was shaped like a ruler and made it easy to calculate using logarithms. This is called a slide rule.
The slide rule was invented in 1632. For more than 300 years it has been used as a calculator to perform complex calculations with ease.
The slide rule is one of those analogue calculators that can calculate not only multiplication and division, but also logarithms, trigonometric functions, square roots, etc. (It is analogue, so the results are approximate, but it is still useful). It was considered a must-have tool for engineers because of its convenience. However, with the advent of functional calculators, they are now rarely used. The picture below shows an example of a slide rule.